|

A PRIMER ON CONNECTIVE GEOMETRY
Space, we
now understand, is not an isolated collection of objects
related in a simple Cartesian matrix. Rather, it
is a rich 4-dimensional field that includes
time and process.
The
constituents of this vast structural field have been
described in a number of ways by physicists and
philosophers. (See for example A.N. Whitehead,
Process and Reality.) The architect and physicist
Christopher Alexander has developed a theoretical
framework in which these constituents can be described
as "centres."
Such centres form regions that are amplified by other
regions, forming perimeter fields with respect to the
centres. This system of centres is embedded in
still-larger systems of centres, with both hierarchical
and network aspects. Each centre is
in fact embedded in the totality of all centres, but
with diminishing contextual influences.
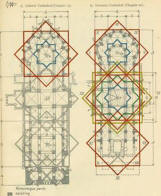

A
simple system of centres -
A much more complex system -
a cathedral plan
the urban fabric of Rome
Process is
central to the understanding of how such centres are
formed, and transformed. The key process is what Alexander calls a "structure-preserving transformation."
(Mathematicians call this transformation
"symmetry-preserving," and they refer to its counterpoint
as
"symmetry-breaking.")
The
formation and transformation of centres results in a
characteristic set of properties that are familiar to
designers. They are structures that resonate
deeply with human experience. The perception of
such underlying order, in fact, gives rise to the human
experience of beauty.
Seen this
way, beauty is less a "constructed" personal experience,
and more a kind of symmetrical interaction between the
person and the larger structure of things. It is
not, therefore, a purely "subjective" phenomenon, but
can be discussed and developed as a collective art.
It is, above all, a perception of natural order.
Alexander identifies 15 such
properties, discussed in great detail in his new book,
The Nature of
Order. We can summarise them here as follows:
15 PROPERTIES OF CENTRE FORMATION



1 Levels of Scale 2. Strong Centres 3. Boundaries



4. Alternating Repetition 5.
Positive Space 6. Good Shape



7. Local Symmetries
8. Deep Interlock
9. Contrast
and Ambiguity



10. Gradients
11. Roughness
12. Echoes


13. The Void 14.
Simplicity and 15. Not Separateness
Inner Calm
The crucial point to grasp is that such a structure of
centres forms a vastly complex connective network in
space. Beyond any symbolic meaning, this structure
embodies real
connective symmetries. It does
so through the exceedingly complex patterns of interactions between
its constituents -- its centres. This greater
complexity arises is in spite of the fact that the steps
of transformation can be deceptively simple.
Thus this very real connective structure carries real and definable (and
discussable) attributes. For example, one can vary
the degree of connectivity, and the density of centres.
In so doing, Alexander argues, one affects the very life
of the structure.
Alexander's aim is that architects and others can use
these insights to structure networks of centres into
more potent classes of connective geometry -- more
beautiful, more coherent human environments. This
offers the ability to create a much richer kind of order
in the built environment of the future.
Following are examples of new dwelling structures
that contain elements of these richly connective classes of
geometry.
Homes in North Africa | 